All numbered problems are from West, 2nd edition.

Homework 9 (due May 1)

Recall that the Petersen graph is vertex transitive, which means that for every pair of vertices $x, y$ there is an automorphism (isomorphism from the graph to itself) that maps $x$ to $y$. See page 14 of West. As a result, any property preserved by isomorphism is the same for all vertices. In this case, $κ(x, y)$ is the same for all pairs of non-adjacent vertices in the Petersen graph.

Let $G$ be the Petersen graph as drawn on Pg 13 of the book whose vertices correspond to the two-element subsets of $[5]$ with adjacencies when the sets are disjoint.
1. As $G$ is vertex-transitive, we may assume $x$ to be any given vertex WLOG, so we will set $x = (12)$. Note there are $10−3−1 = 6$ vertices in $G$ not adjacent to $(12)$. By the clear symmetry in the drawing on Pg 13, it will be enough to compute $κ((12), (23)), κ((12), (13)), κ((12), (41))$. Compute these three quantities by exhibiting suitable x, y-cuts and showing their optimality by finding and drawing sets of internally disjoint $x, y$-paths of the same size. Based on your answers, what is $κ(G)$?
2. What is $κ_e(G)$? (Hint: use theorem 4.1.9 or 4.1.11).
We showed that $κ(Q_k ) = k$ for $k ≥ 2$, where $Q_k$ is the hypercube graph.
1. Given a pair of non-adjacent vertices $x, y$ in $Q_k$, what is the maximum number of pairwise internally disjoint $x, y$-paths? Fully justify.
2. Explicitly show by example that your answer is correct on $Q_3$
Defined on pg. 166: For $X, Y ⊆ V (G)$, an $X, Y$ -path is a path having first vertex in $X$, last vertex in $Y$, and no other vertex in $X ∪ Y$. In the following, you will prove the $S, T$-path theorem: for any k-connected graph G, if S and T are disjoint subsets of V (G) with size at least k, then we can find k pairwise disjoint S, T -paths in G. Note: these paths are not just internally disjoint; they cannot share endpoints either.
1. Read the Expansion Lemma 4.2.3 in the book, pg. 162. Add a new vertex $u$ adjacent to every vertex in S and a new vertex v adjacent to every vertex in T and call the resulting graph $G′$ . What does the expansion lemma tell us about $G ′$?
2. Apply Menger’s theorem to $u, v$ in $G′$ and finish the proof of the $S, T$ -path theorem.
Given a (undirected) graph G, recall that the line graph L(G) is defined as the simple graph whose vertex set V (L(G)) is the same as the edge set of G, E(G). Two distinct edges e, f in G viewed as vertices of L(G) are adjacent in L(G) if and only if e and f are incident to a common vertex in G.
1. Characterize the graphs G which have line graph L(G) equal to the empty graph.
2. Let $n ≥ 3$. What standard graphs are $L(P_n)$ , and $L(C_n)$ and $L(K_{1,n})$ isomorphic to?
3. For the graph below, draw the line graph.

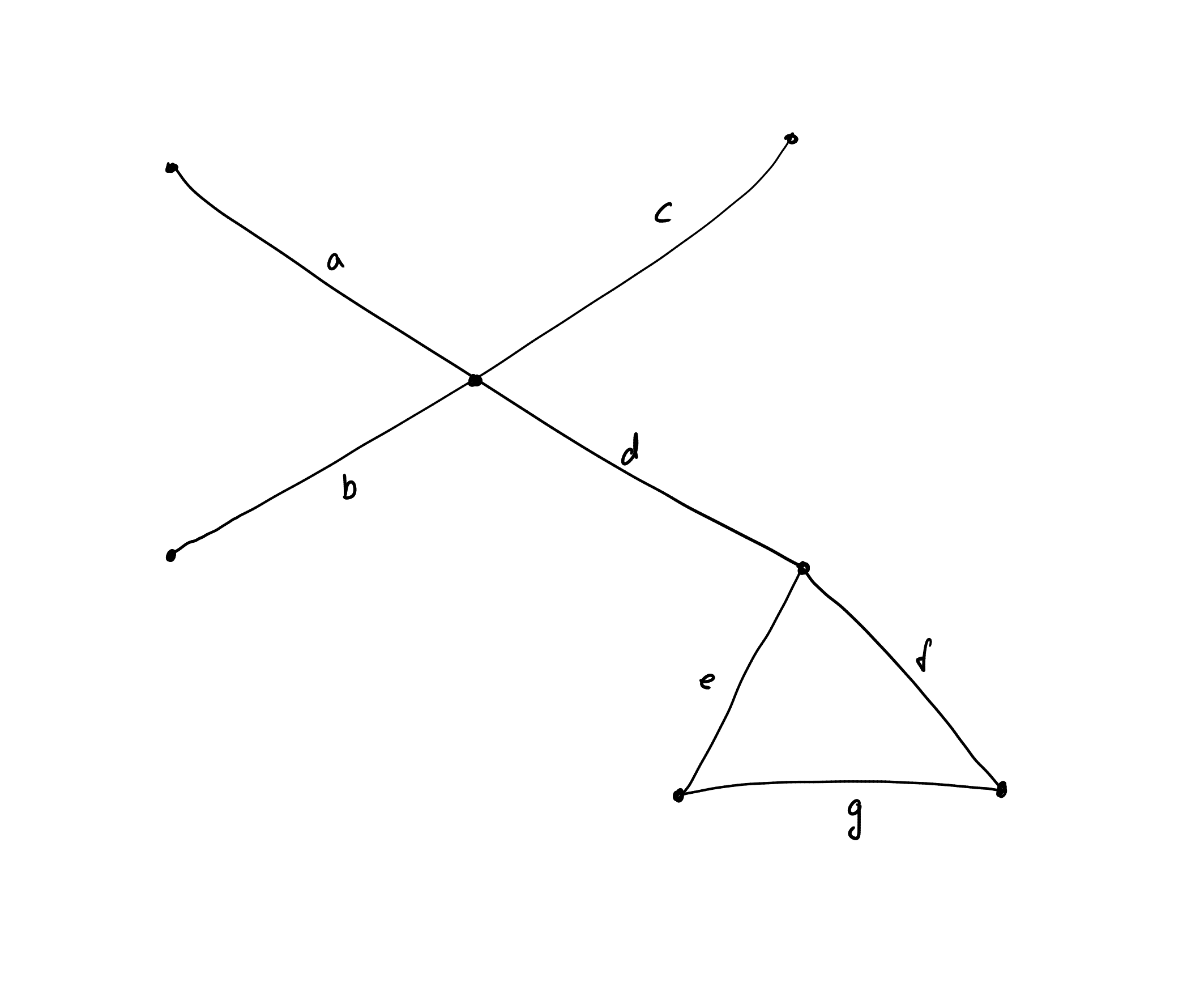
hw9fig1

Homework 8 (due Apr 21)

Do problems 1-4 from attached HW8

Homework 7 (due Apr 11)

Let $Q_k$ be the k-dimensional hypercube.
1. Use induction to prove that for $k ≥ 2$, $Q_k$ has at least $2^{2^{k−2}}$ perfect matchings.
2. The Hamming weight of a vertex in $Q_k$ is the number of 1s in its label. For example, in $Q_3 , v = (0, 0, 0)$ has Hamming weight $0$ and $w = (1, 0, 1)$ has Hamming weight $2$. How many vertices of $Q_k$ have Hamming weight $j$?
3. Prove that for every perfect matching in $Q_k$ , the number of edges matching vertices with Hamming weight $i$ to vertices with Hamming weight $i + 1$ is $\binom{k-1}{i}$, for $0 ≤ i ≤ k − 1$. Hint: Use induction on $i$. If a vertex with Hamming weight $i$ is not matched to a vertex with Hamming weight $i + 1$ then it is matched to a vertex with Hamming weight $i − 1$.
Recall that $\maxM(G)$ denotes the maximum size of a matching in G. Suppose that $\tilde{M}$ is a matching in $G$ with less than $\maxM(G)/2$ edges. Show that if $M$ is a maximum matching in $G$, then there is an edge $e ∈ M$ such that $\tilde{M} + e$ is a matching in $G$. Explain why every maximal matching in $G$ must have $\maxM(G)/2$ edges.
Using nonnegative edge weights, construct a 4-vertex weighted graph in which the matching of maximum weight is not a matching of maximum size.
Use the augmenting path algorith to find a maximum matching and minimum vertex cover in the bipartite graph whose adjacency matrix is:

$\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0\\ \end{bmatrix}$

Note: Be sure to use augmenting path algorithm even though it may be possible to find a maximum matching simply by inspection since this graph is small.

Homework 6 (due Mar 26)

2.2.6
2.2.7
2.3.5
2.3.13

Homework 5 (due Mar 19)

Let $G$ be a graph with $n$ vertices and $m$ edges. Prove that if $m\geq n$, then $G$ has at least $m-n+1$ cycles.
Let $k\geq 2$. Suppose $T$ is a tree with $n$ vertices, $k$ leaves, and $\Delta(T)=k$.
1. Show that $T$ decomposes into $k$ paths with a common endpoint.
2. Find the minimum and maximum values of $\mbox{diam}(T)$ in terms of $n$ and $k$ and draw representative examples attaining these values.
In problem 2.1.62, given a connected graph $G$ with $n$ vertices, a new graph $G'$ is constructed as follows: for each spanning tree of $G$, we draw a vertex in $G'$. Vertices in $G'$ are adjacent if and only if the corresponding spanning trees in $G$ have exactly $n-2$ common edges (or equivalently, only differ by one edge). Answer the questions below (do not do 2.1.62 as written, although it might be helpful to consider the example drawn there).
1. Suppose $G=C_3$ with edges $e_1, e_2, e_3$. There are 3 spanning trees (obtained by deleting one edge) leading to 3 vertices in $G': t_1=\{e_1,e_2\}, t_2=\{e_1,e_3\}, t_3=\{e_2,e_3\}$. All pairs $t_i, t_j$ are adjacent since they only differ by one edge, therefore $G'=C_3$. Show more generally that if $G=C_n$, then $G'=K_n$.
2. Show more generally that if $C_m$ is a subgraph of $G$, then $G'$ contains the clique $K_m$. (Careful here: If $\vert V(G)\vert >m$ you need to think more about how spanning trees can differ).
3. Find $G'$ for the path $G=P_n$. Now finish the following sentence appropriately: “If $G$ is a tree, then…”
4. Prove that if $\vert V(G')\vert \geq 2$, then $G'$ has no isolated vertex.
5. Prove that $G'$ is connected. Hint: let $t_1, t_2$ be vertices in $G'$ corresponding to spanning trees $T_1\neq T_2$ of $G$. To walk from $t_1$, cut an appropriate edge from $T_1$, then add an appropriate edge from $T_2$. If you do not arrive at $t_2$, what do you do?
In general, a metric space is a set $X$ with a metric defined on the set. A metric $d$ is a notion of distance which must satisfy the following three properties:
1. $d(u,v)\geq 0$ for all $u,v \in X$ with equality iff $u=v$.
2. $d(u,v)=d(v,u)$ for all $u,v \in X$.
3. $d(u,v)\leq d(u,z)+d(z,v)$ for all $u,v,z \in X$. (triangle inequality)
1. For a graph $G$, the distance $d(x,y)$ defined for $x, y \in V(G)$ on page 71 is a metric. Verify that (i) and (ii) are satisfied. Show that the triangle inequality $(iii)$ holds.
2. Use part (a) to prove that for any graph $G$, $\mbox{diam}(G)\leq 2\mbox{rad}(G)$.

Homework 4 (due Mar 5)

Let $d_1, \dots, d_n$ be a list of nonnegative integers with even sum and whose largest entry is strictly less than $n$ and differs from the smallest entry by at most $1$, e.g., $4,4,4,3,3,3,3$ or $5,5,5,5,4,4,4,4,4$. Show that any such sequence is a graphic sequence i.e., is the degree sequence of some simple graph.
Let $A$ be an alphabet of size $k$ say $\{1, \dots, k \}$. Let $B_n(k)$ be a generalized de Bruijn digraph defined as follows: The vertex set $V$ is given by $V=\{ \text{ A-sequences of length } n \}$ and there is a directed edge from $a_1 \dots a_n \to a_2 \dots a_n c$ labelled $c$ for $c=1,2, \dots k$.
1. What are the number of vertices and edges for $B_n(k)$? What are the in-degree and out-degree of vertices in this digraph?
2. Explain why $B_n(k)$ is strongly connected and why it must have an Euler circuit.
3. Explain why if the edge labels of an Euler circuit of $B_n(k)$ are laid out on a circle/cycle, they would have the property that every $A$-sequence of length $n+1$ would occur exactly once in this cycle.
Let $T$ be a tournament with no vertex of indegree $0$ (i.e. no player beat every other player).
1. Prove that if $x$ is a king in $T$, then $T$ has another king in $N^{-}(x)=\{ \text{ predecessors of } x \}$.
2. Use this to prove $T$ has at least $3$ kings.
3. For each $n \geq 3$ construct a tournament with $\delta^{-}(T) > 0$ and only $3$ kings.
For a loopless (undirected) graph $G$, a matrix that comes up often is the Laplacian matrix $\mathbb{L} = \mathbb{D} - \mathbb{A}$ where $\mathbb{D}$ is a diagonal matrix with diagonal entries the degrees of vertices in $G$ (with respect to some vertex ordering) and $\mathbb{A}$ is the adjacency matrix of $G$ (with respect to the same vertex ordering).
1. Show that $\begin{bmatrix} 1 \\ \vdots \\ 1 \end{bmatrix}$ is an eigenvector of $\mathbb{L}$. What is the corresponding eigenvalue? Explain how your result shows that $\mathbb{L}$ is always singular i.e. $det(\mathbb{L})=0$.
2. If $G$ is a $d$-regular graph, explain why the spectrum of $\mathbb{L}$ and the spectrum of $\mathbb{A}$ are related by $Spectrum(\mathbb{L}) = d - Spectrum(\mathbb{A})$ i.e., $\lambda$ is an eigenvalue of $\mathbb{A}$ of multiplicity $m$ if and only if $d-\lambda$ is an eigenvalue of $\mathbb{L}$ of multiplicity $m$.
(The Laplacian comes up in applications of graph theory to probability and physics - it is always good to check when reading an application involving the spectrum of a graph to see whether the spectrum of the adjacency matrix or Laplacian is meant. When the graph is regular you have shown that they are easily obtainable from each other but for general graphs the relationship is more subtle. We will see one application of the Laplacian in the Matrix Tree Theorem coming up soon in the chapter on Trees.)

Homework 3 (due Feb 20)

HW 3

Solutions for corrected problems

Homework 2 (due Feb 8)

HW 2

Solutions for corrected problems

Homework 1 (due Jan 30)

Solutions

1.1.4 (Two graphs are isomorphic iff their complements are)
1.1.11 (Determine maximum size in a clique and maximum size of an independent set in a particular graph)
1.1.14 (Removing opposite corners of a checkerboard, and then domino tiling it)
1.1.15 (Determine isomorphism classes of graphs that are both paths and cycles, complete graphs that are also bipartite, and so on. A total of 6 pairs)
1.1.19 (Determine if given graphs are isomorphic or not)
1.1.29 (Prove that every set of six people have at least 3 mutual acquaintances or 3 mutual strangers)
1.1.30 (Interpret $A^2$ and $MM^T$ where $A$ and $M$ are the adjacency and incidence matrix respectively)
Prove or disprove
1. If every vertex of a simple, connected graph has degree 2, then G is a cycle.
2. What if we remove the word “connected” in part (a).
Recall definition 1.1.39: the girth of a graph with a cycle is the length of its shortest cycle. A graph with no cycle has infinite girth. Let $G$ be a graph with girth 4 in which every vertex has degree $k$.
1. Explain why $G$ must be a simple graph. Hint: loops are cycles of length 1.
2. Prove that $G$ has at least $2k$ vertices.
3. Prove that if $G$ has exactly $2k$ vertices, then it is isomorphic to the complete bipartite graph $K_{k,k}$ , $k ≥ 2$.